Quadratic Equation
A Quadratic equation is a second-order polynomial equation in a single Variable x,
Ax2 + bx + x = 0
with a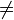 
0. Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has two solutions. These solutions may be both real, or both complex.
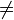0. Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has two solutions. These solutions may be both real, or both complex.
The roots x can be found by completing the square,
X = {-b
(b2
– 4ac)}/2a
This equation is known as the quadratic formula.
b2 - 4ac is often
called Discriminant.
D = b2 - 4ac
Case 1: D > 0
Two unequal real roots
Case 2: D = 0
Two equal real roots
Case 3: D < 0
Complex roots
Besides this you need to remember root Relationship:
Let's assume ax2 + bx + x = 0 is the quadratic equation and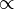 
and β are the two roots, then we can always write like:
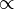and β are the two roots, then we can always write like: 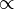+ β = -b/a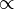β = c/a
Remainder Theorem
To identify whether a given expression is a factor of another expression, we can take help of Remainder Theorem.
According to the remainder theorem, when any expression f(x) is divided by (x - a) the remainder is f(a), (a is any constant in this example).
Thus, When the expression x2 + 5x + 4 is divided by x +1, reminder will be
f(-1) = (-1)2 + 5(-1) + 4
f(-1) = 1 - 5 + 4
f(-1) = 0
Here reminder is zero also means (x +1) is a factor of the given equation.
Questions and Solutions
1. Find the roots of quadratic equation: 3x2 - 7x - 6 = 0?
Sol:
3x2 - 9x - 2x - 6 = 0
3x(x - 3) + 2(x - 3) = 0
(x - 3)(3x + 2) = 0
⇒ x = 3, -2/3
2. Find the sum and product of the roots of the quadratic equation: x2 + 2x - 15 = 0?
Sol:
x2 + 2x - 15 = 0
ax2 + bx + c = 0
a = 1, b = 2, c = - 15
Product of roots = c/a = -15
Sum of roots = -b/a = -2
3. What is the nature of roots of the equation 3x2 - 12x + 10 = 0?
Sol:
The discriminant of the quadratic equation is
D = (-12)2 - 4(3)(10) = 24
As this is positive but not a perfect square, the roots are irrational and unequal.
4. For what values of k, the equation x2 + 2(k -4)x + 2k = 0 has equal roots?
Sol:
The roots are equal, we have D = 0.
D = b2 - 4ac = 0
4(k - 4)2 - 8k = 0
⇒ (k - 4)2 - 2k = 0
⇒ k2 - 10k + 16 = 0
⇒ (k - 8)(k - 2) = 0
⇒ k = 8 or k =2
5. Find the remainder when x2 - 2x - 3 is divided by x + 1 using the remainder Theorem.
Sol:
f(x) = x2 - 2x - 3
x + 1 ⇒ x = -1
for finding the remainder
f(-1) = (-1)2 -2(-1)-3
= 1+2-3 = 0
remainder = 0
Also on:-